11.5.2.6 to understand the time-efficiency of algorithms 

11.5.2.7 to understand the space-efficiency of algorithms 

Algorithm efficiency

Algorithm complexity is just a way to formally measure how fast a program or algorithm runs.

Let's consider two algorithms, which both calculate the sum of the first n integers.

Which algorithm is more efficient? Why?

Time efficiency of algorithm

Algorithms may be compared on how much time they need to solve a particular problem. 
This is referred to as the time complexity of the algorithm. 

The goal is to design algorithms which will run quickly.

In order to compare the efficiency of different algorithms in terms of execution time, we need to quantify the number of basic operations or steps that the algorithm will need, in terms of the number of items to be processed.

Time efficiency is measuring the number of seconds an algorithm takes to complete. 

Time taken - the number of steps in the algorithm. 

Big O

Big O notations are used to measure how well a computer algorithm scales as the amount of data involved increases.

Big-O establishes a worst-case run time

Another mathematical concept used by Big-O is permutations. Permutation relates to the act of arranging all the members of a set into order (described by factorial - meaning that if we need to put N members in order this can be done with N! ways).

Permutation is a mathematical calculation of the number of ways a particular set can be arranged, where order of the arrangement matters

O(1) (Constant time)

O(1) describes an algorithm that takes constant time (the same amount of time) to execute regardless of the size of the input data set.

Suppose array a has n items. The statement
length  <-- len(a)
will take the same amount of time to execute however many items are held in the array.

O(n) (linear time)

O(n) describes an algorithm whose performance will grow in linear time, in direct proportion to the size of the data set. For example, a linear search of an array of 1000 unsorted items will take 1000 times longer than searching an array of 1 item.

input key
for i=1 to n
    if a[i]=key then break
endfor

How many comparisons in the worst case?

O(n²) (Polynomial time)

O(n²) describes an algorithm whose performance is directly proportional to the square of the size of the data set. A program with two nested loops each performed n times will typically have an order of time complexity O(n2). The running time of the algorithm grows in polynomial time.

O(log n) (Logarithmic time)

The time taken to execute an algorithm of order O(log n) (logarithmic time) will grow very slowly as the size of the data set increases.  Doubling the size of the data set has very little effect on the time the algorithm takes to complete. (Note that in Big-O notation the base of the logarithm, 2 in this case, is not specified because it is irrelevant to the time complexity, being a constant factor.)

O(n!) (Exponential time)

The time taken to execute an algorithm of order O(n!) will grow very quickly, faster than O(2n). Suppose that the problem is to find all the permutations of n letters. If n=2, there are 2 permutations to find. If n=6, there are 720 permutations - far more than 2n, which is only 64.

Space efficiency of algorithm

Spaсу efficiency of an algorithm is the use of the minimum amount of resources such as memory

Space used - the amount of data that the algorithm needs to keep track of at once.   

First example "Swapping data"

Second example "Look through the items in the list"

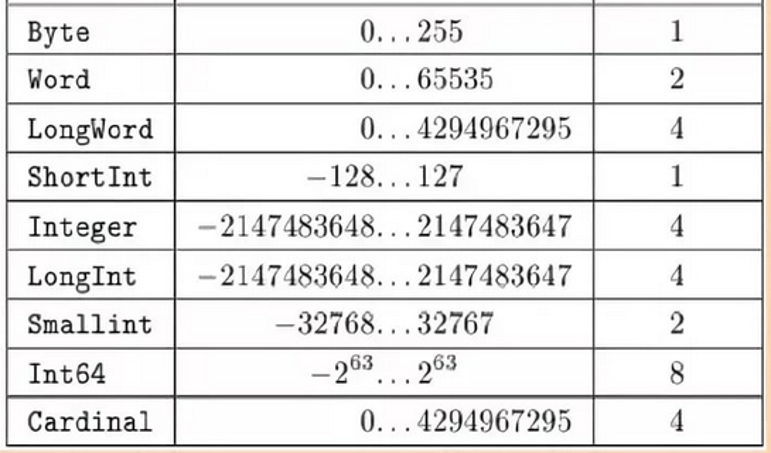
Choose data type

When we use different variable we define data type for variable.

Which data type appropriate for code symbol of ASCII.

Why would other types of data be inefficient to use?

Questions:

1. Give definition for term "algorithm complexity".
2. Explain the main idea in time efficiency algorithm.
3. Explain what space efficiency algorithm is.
4. What describes Big-O notation.

Exercises:

Ex. 1 Algorithm complexity (Author: Litvinova Olga CS teacher of NIS Pavlodar)

Ex. 2 Quiz "Algorithm efficiency" (Author: Litvinova Olga CS teacher of NIS Pavlodar)

Exam questions: